YOU SHOULD PROBABLY NOT START WITH THIS PAGE.
 

ZIGZAG® PARADOXES tm

That's how it works.  While we can create straightforward structures, we can also create some very strange ones.

A paradox is in your mind, when an expectation is violated.  But in ZigZag you may not get what you expected in ordinary 3D space, or 2D paper space.

For instance, consider the looping rank (ringrank):

... A - A - A ....

This is certainly unlike anything in the spaces of our ordinary lives.

For a richer example, consider these arrangements of cells (from "The Axioms of ZigZag Structure" ).

   A - B - C - D - E - F

R - L - Q

A - B - C - R
... A - A - A ....

What isn't mentioned in "The Axioms of ZigZag Structure" is that ALL THESE RELATIONS ARE POSSIBLE AT THE SAME TIME.

Why?  Because a cell's interconnections in one dimension are completely independent of its interconnections in another.

It's not like that in our more familiar spaces, like paper or 3D.

On a spreadsheet, for example, a cell's horizontal connections may prevent it from turning up on an entirely different part of the spreadsheet.  But in ZigZag, that's easy.

One of the most exciting properties of ZigZag space is this:

ANY NUMBER OF CELLS CAN OCCUPY THE SAME INTERSECTION.

That is, at the intersection of any two ranks you can have lots of different cells at the same time.

Let's prove it for two.  Consider a rank in d.1 with headcell A (the negmost cell in d.1) and a rank in d.2 with headcell B (the negmost cell in d.2).

It is obvious that there is a cell at the intersection of A and B.  Let us be more explicit, and label the first cell at the intersection C:

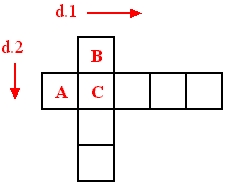
To see it more clearly, let's put a cursor on cell C:

However, it is less obvious that another cell, D, can be in both ranks at the same time.

The ranks are doubly-crossed, or, if you will, double-crossed.  Moving the cursor will clarify it.  If we put the cursor on that cell it looks like this:

But if we go to another refresh-- the "columns" refresh, or H view-- it will look like this whether the cursor is on C or D:

You could now go to any of the pages--

"The Connections of ZigZag"
"The Views of ZigZag"
"The Axioms of ZigZag Structure"
"The Multidimensionality of ZigZag"
"Special Properties of ZigZag Structure"
"Easy Misunderstandings about ZigZag"