 tm
tmPreamble to Axiom 1 (from "The Connections of ZigZag"). Cells are connected. A series of two or more cells connected along any dimension is a rank.The Axioms of ZigZag® Structure tm
AXIOM 1
In any dimension,
a cell can have at most one neighbor in each direction.Examples.
A - B - C - D - E - F
Here we see that A has a neighbor in the positive (posward) direction of dimension 1, but no neighbor in the negative (negward) direction. B, C, D and E all have both a posward and a negward neighbor. F has a negward neighbor but no posward.
R - L - Q
Here R has no negward neighbor in dimension 3, Q has no posward, L has both.
A - B - C - R
Here in dimension 17, A has no negward neighbor, R has no posward, and B and C have both negward and posward neighbors.
Another example:
... A - A - A ....
In this example, in dimension 3 cell A is connected to itself in a loop. It has one neighbor, itself, on each side.
Preamble to Axiom 2. Since a dimension has a positive direction and a negative direction,

every cell has a positive side and a negative side in each dimension,
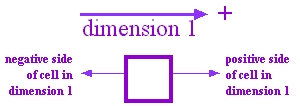 which
are important to its connective structure.
which
are important to its connective structure.
Note that it would be possible to fit Axiom 1 and 2 into a single axiom, but it would probably be much harder to understand.AXIOM 2
In any dimension,
a cell's positive side may only connect to a cell's negative side, and vice versa.Examples.
A - B - C
A's positive side on dimension 1 connects to B's negative side on dimension 1. B's positive side on dimension 1 connects to C's negative side on dimension 1.
... A - A - A ....
In this example, the negative side of cell A is connected to its own positive side, and vice versa.
While these examples were given before in the context of Axiom 1, they are explained differently in the context of Axiom 2.
Back to WELCOME TO ZIGZAG. .
If you haven't already seen these, try 'em now:
"The Connections of ZigZag"No doubt by now you're ready for "Special Properties of ZigZag Structure".
"The Views of ZigZag"
"The Multidimensionality of ZigZag"
You may want to look at "Easy Misunderstandings about ZigZag".
And if you're daring, go for "The Paradoxes of ZigZag".