THE CONNECTIONS of ZigZag® tm

Consider a list, or a checkerboard, also called a spreadsheet,

or hierarchical directories on a computer.

Each of these is an arrangement of discrete connections.

We have generalized these connections in a new and unusual way which is VERY SIMPLE and yet VERY HARD TO EXPLAIN.  (These two properties are signs of a new paradigm.)

These connections exist in a kind of connective space.  But this is NOT like the x-y space you learned about in high school.  Connective dimensions are different, as you will see.  (For instance, it doesn't make sense to talk about "distance" between items, only connections between them.  And it gets stranger.)

Let's start the explanation with the spreadsheet.   A spreadsheet is two-dimensional.  That is, it has rows (the horizontal dimension) and columns (the vertical dimension).  The horizontal dimension has a positive and negative direction,

and the vertical dimension has a positive and negative direction.*

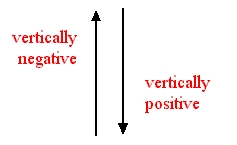* Note that this negative direction doesn't go the same way as the "y" coordinate you learned about in high school.  That's because traditionally the spreadsheet rows are assigned larger and larger numbers as they go DOWN, not up.  (This is just a labelling convention, though, and you'll be able to reverse the views to your heart's content as you use ZigZag.)

That gives us two dimensions.

So the basic arrangements can't be rows and columns, because that would only allow only two dimensions.  So instead we'll use the term RANK*.

* This usage is borrowdd from Kenneth Iverson's APL language.

A rank is a series of cells connected along some dimension.

For instance:

Here's a rank of five cells, viewed horizontally:

We're not saying here what dimension it's on.  But note that if we see a rank horizontally, we call it a ROW, regardless of which dimension it's connected along.

Now here's rank of three cells, viewed vertically:

We're not saying here what dimension this rank is on, either.  But note that if we see a rank vertically, we call it a COLUMN, regardless of which dimension it's connected along.

Cells can even be connected in loops
.

Consider this one of the ZigZag paradoxes.

Now you're ready for the ZigZag AXIOMS.

Or maybe you'd rather read about "The Views of ZigZag".  Or ZigZag multidimensionality.

Back to WELCOME TO ZIGZAG.    .